Runtime Analysis: Sets vs Maps vs Sorting

The basis of comparing two algorithms comes down to a simple fact, how does their time & space complexities compare. There are different ways in which we may express these, with the most commonly used one being O-_notation(Big-Oh). In short, the _O-notation tells us about the worst-case complexity. But it doesn't necessarily convert to real-life circumstances where it's not the worst-case every time.

While complexity analysis is a great tool, it often doesn't tell us the whole truth. Today we will be comparing the actual efficiency of set and map data structures while comparing it to the sorting algorithm.

Sets vs Sorting:

Many problems can be solved either by using sets or by sorting and one such problem is finding out how many unique elements there are in the given data.

One way to solve this problem would be to insert every element in the set and return the size of the set. Here we can also use unordered_set because the order of elements doesn't matter. Another way would be to sort the given vector and count the number of occurrences where two consecutive elements are different. The time complexity of both the solutions (with a set or with sorting) is O(n log n).

Let's see how they compare.

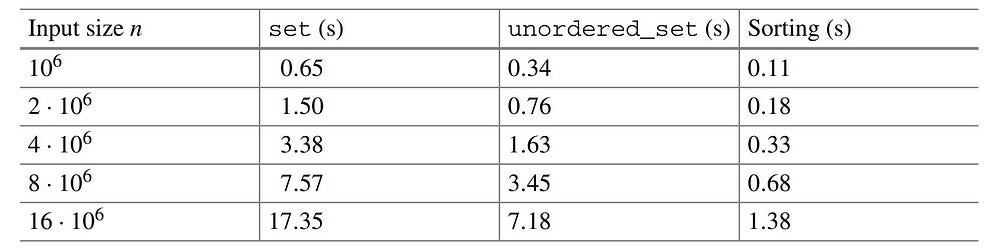
Table showing the time taken by set, unordered_set & sorting for the same task.

We see that solving the same problem with a set takes more than twice the time as it would take if we would have used an unordered_set. And it's about ten times slower as compared to sorting. Even though they have the same time complexity there is wide variation in the time taken and it will only increase if we increased the data size.

Maps vs Sorting:

Maps are used to store key-value pairs and they are very convenient to use. Here we will generate some random numbers and calculate the frequency of each number. This task can also be done with vectors. The time complexity of both the solutions is O(n log n).

Let's see how they compare.

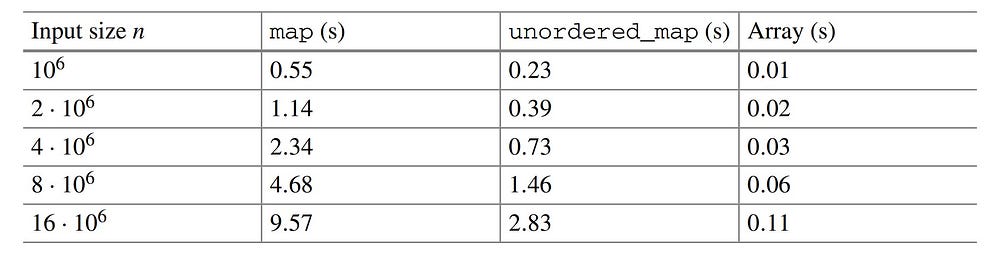
Table showing the time taken by map, unordered_map & sorting for the same task.

We see that unorderedmap is about three times faster than map and it is expected too because of _O(1) per operation in the former one as compared to the O(log n) per operation in the latter one. But still, we see that using sorted vectors is about 25 times faster than unordered_map and about 87 times faster than using map.

Why?

We see similar trends in both comparing sets with sorted vectors and maps with sorted vectors. In both cases sorted vector outperformed by a great margin. But why is this so?

A possible answer is that the constant factors that we neglect while calculating the time complexity of set & map are much greater than those present in sorting. Also sorting is a very basic computational operation while set and map both are made up using very complex underlying data structures(e.g. RB Trees and pairs) and hence they are more expensive.

Thank you for reading the article. I hope you found it interesting & insightful. Follow for more such articles.